|
PHOTONIC BOMB
|
RANDOM LASER
|
EMISSION SPECTRA OF ORGANIC RANDOM LASER
|
SPECKLE PATTERN
|
RANDOM LASERS
In recent years, random lasing materials (e.g. powders, porous media, precipitates in solution, or photonic crystals with impurities) have been extensively studied experimentally. Pumping energy into these systems causes them to re-emit multi-mode coherent light, with a spectrum displaying randomly arranged peaks in frequency. Starting from the structure and
geometry of the atoms and molecules that scatter the light waves, one would eventually want a theory that predicts the onset, the nature and the features of the light modes and answering the following questions:
A key challenge that we address is the characterization of the structure of this network of modes and the strengths of the relevant random interactions, as is required, e.g., in order to distinguish apart physical regimes of laser behavior.
In recent years, random lasing materials (e.g. powders, porous media, precipitates in solution, or photonic crystals with impurities) have been extensively studied experimentally. Pumping energy into these systems causes them to re-emit multi-mode coherent light, with a spectrum displaying randomly arranged peaks in frequency. Starting from the structure and
geometry of the atoms and molecules that scatter the light waves, one would eventually want a theory that predicts the onset, the nature and the features of the light modes and answering the following questions:
- where do light modes localize, if they do localize at all ?
- what shape and size do light modes display in space ?
- on which frequencies do light modes emit in cavity-less media?
- what is (is there) a random laser pulse in time ?
- do competing laser modes phase-lock as in multimode standard cavity lasers ?
- how strong is the coupling magnitude and how is it related to the coupling modes spatial overlap ?
A key challenge that we address is the characterization of the structure of this network of modes and the strengths of the relevant random interactions, as is required, e.g., in order to distinguish apart physical regimes of laser behavior.
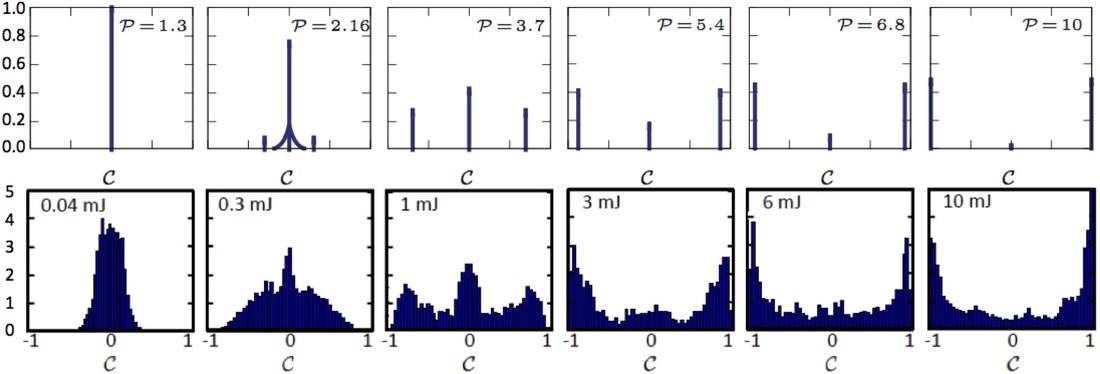
GLASSY RANDOM LASER AND EXPERIMENTAL MEASUREMENT OF REPLICA SYMMETRY BREAKING
INFERENCE OF COUPLING OF WAVES IN RANDOM MEDIA
The light modes interaction network has to be inferred starting from data acquired in measurements, of spectra and correlations of phases and amplitudes of the light modes, and this inference problem is closely analogous to those in our other areas of application of statistical inference. Our inference project is concerned with the bottom-up approach for studying statistical models for application to wave and optics. The parameters describing a given model system, like active links in the network system under consideration and external field affecting the system, are inferred utilizing the data set (intensities and phases configurations, spatial correlations among sites, coherency degrees, order parameters, etc.) which is made available once the system is studied numerically (by simulations) or experimentally. Various inference techniques are employed to achieve this task, Mean Field approach, TAP extension to mean field approach, Adaptive TAP, Pseudo Likelihood Maximization (PLM) with L2 regularization and PLM with decimation. Such inverse problems for network reconstruction are considered on various graphs like 2D and 3D lattices and Bethe and Erdos-Renyi sparse random graph. Both ordered and disordered systems are studied under the influence of external field and otherwise. Alongside real links/couplings in the system, also complex Hermitian couplings are taken into consideration.
The light modes interaction network has to be inferred starting from data acquired in measurements, of spectra and correlations of phases and amplitudes of the light modes, and this inference problem is closely analogous to those in our other areas of application of statistical inference. Our inference project is concerned with the bottom-up approach for studying statistical models for application to wave and optics. The parameters describing a given model system, like active links in the network system under consideration and external field affecting the system, are inferred utilizing the data set (intensities and phases configurations, spatial correlations among sites, coherency degrees, order parameters, etc.) which is made available once the system is studied numerically (by simulations) or experimentally. Various inference techniques are employed to achieve this task, Mean Field approach, TAP extension to mean field approach, Adaptive TAP, Pseudo Likelihood Maximization (PLM) with L2 regularization and PLM with decimation. Such inverse problems for network reconstruction are considered on various graphs like 2D and 3D lattices and Bethe and Erdos-Renyi sparse random graph. Both ordered and disordered systems are studied under the influence of external field and otherwise. Alongside real links/couplings in the system, also complex Hermitian couplings are taken into consideration.